|
|
|||||
| |
|
|
|
|
|
|
| |
|
|
||||

S ay
each integer aloud or to yourself.
"Let's see, I have four numbers, I need to say each of them to myself. The first number is negative three and six tenths, the next is two and eight tenths, the third is negative one and two tenths, and the last one is one and five tenths. "
P oint to each integer and look for negative signs.
- Check for & circle negative integers by looking for the "-" symbol.
- Integers that are positive will likely not have a sign.
![]()
"Let me look at the numbers again. 2.8 and 1.5 do not have negative signs, but 1.2 does and so does 3.6. That means that both 1.2 and 3.6 are negative numbers, so I will circle 1.2 and 3.6."
I dentify whether each integer is positive or negative.
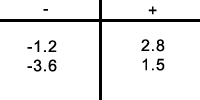
- Look at the circled numbers. You might want to draw a chart like this:
- Then you can put the numbers in each column.
"I've circled two numbers- 1.2 and 3.6. I will write them in the - column. The other two numbers, I will write in the + column."
E stimate the value of each integer using the Rules of Value.
- Rules of Value
- Rule #1 (positive # & negative #) - positive integer is always greater in value.
- Rule #2 (all positive #'s) - integer that is farther from zero on a number line is of greater value.
- Rule #3 (all negative #'s) - integer closest to zero on a number line is of greater value.
-
Draw a number line to help you to use the Rules of Value.
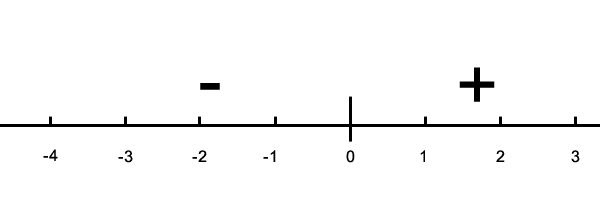
"Let me see. I will draw a number line to help me estimate. I will put zero in the middle, and just like my t table, put a + on the right and a - to the left of the zero."
-
Use the rules to put the numbers on the number line and measure their distance from zero.
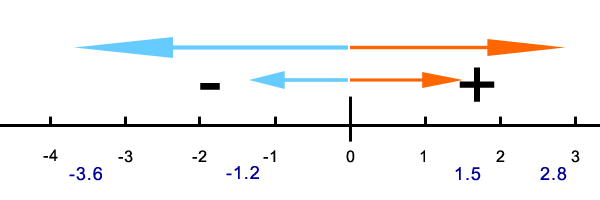
"Rule #1 says that positive integers are always greater. I have two positive integers, 2.8 and 1.5 so I will put them on the number line first. I know that these two will be larger than the two negative numbers, -3.6 and -1.2." Rule # 2 says that with positive numbers, the integer farther from zero is of greater value. For the two positive integers, if I draw a line from zero to each of them, 2.8 is farthest away from zero. Using this rule, 2.8 is the largest of the two positive numbers. For negative numbers, it's opposite of positive numbers. Rule # 3 says with negative numbers, the integer closest to zero is of greater value. For the two negative integers, if I draw a line from zero to each of them, -1.2 is closest to zero. Using this rule, -1.2 is the larger of the two negative numbers."
S elect integer of greatest value.
- Number the integers on your number line from in order from largest to smallest.
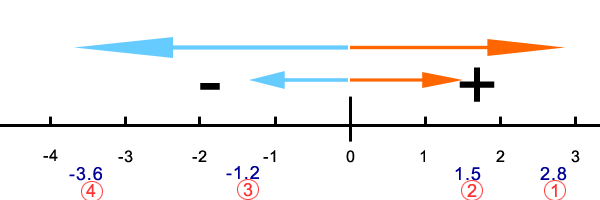
" I know that positive numbers are larger, and that 2.8 is the largest of the positive numbers. I am going to put a #1 under 2.8, and a #2 under 1.5.Then I am going to look at my negative numbers. Using Rule # 3, I know that -1.2 is larger than -3.6 because, -1.2 is closer to zero on the number line. So, I am going to put a #3 under -1.2 because it is the third largest number. It is smaller than 2.8 or 1.5 because it is negative, but it is larger than -3.6 because it is closer to zero on the negative side of the number line. Finally, I am going to put a #4 under -3.6 because it is the smallest number. It is a negative number and it is furthest away from zero on the negative side of the number line.
-
Write the integers in order according to the circled numbers on the number line.

"So my integers in order, largest to smallest are: 2.8, 1.5, -1.2, -3.6"
| |
|
|
|
|
|
|
|
| |
 |
||||||
|
|
|
||||||
| |
|
||||||
| |
|
|
|
|
|||
| |
|
|
|||||